مقدمه
هنگامی که قصد تحلیل یک سری بزرگ از داده ها وجود دارد طبقه بندی به ما کمک خواهد کرد، زیرا که طبقه بندی روشی استاندارد برای نظم دادن به داده ها می باشد. می توان گفت که با این کار، داده ها به شکل قابل استفاده و ساده تر بیان می شوند و اعضای مشابه در کنار هم قرار می گیرند. در این مطلب به روش هایی برای طبقه بندی کردن داده ها با دیدگاه آماری و مکانی پرداخته شده است.
طبقه بندی داده ها با روش آماری
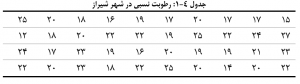
گاهی اوقات آنقدر داده هایی که با آنها سر و کار دارد، از نظر تعداد زیاد هستند که فرد دچار سردرگمی می شود، بنابراین آنها را در قالب جدول فراوانی، می توان به شکل منظمی در آورد. در جدول زیر رطوبت نسبی شهر شیراز از سال ۱۳۵۰ تا سال ۱۳۸۹ به صورت زیر درج شده است.
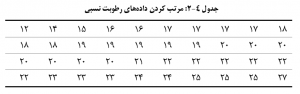
ساده ترين راه تنظيم آماری داده ها مرتب كردن آنها به صورت صعودي (نزولي) است. اين كار در جدول ۴-۲ انجام شده است. از اين جدول با زحمتي كمتر می توان فهميد كه کمترین و بیشترین مقدار رطوبت در شهر شیراز کدام است؟ مقدار تفاوت بين آنها چقدر است.
برای طبقه بندی کردن داده ها باید چند گام را انجام داد که به شرح زیر است:
– تصمیم گیری درباره تعداد طبقات
تصمیم گیری راجع به تعداد طبقات باید با دقت انجام شود. اگر تعداد طبقات کم انتخاب شود، گرچه انجام محاسبات ساده تر خواهد بود ولی اندازه های کمی به صورت فشرده در آمده و اطلاعات مورد نظر با دقت لازم به دست نخواهد آمد. بالعکس اگر تعداد طبقات زیاد انتخاب شود ضمن اینکه محاسبات و نتیجه گیری مشکل خواهد شد نتیجه ای که از رده بندی مورد نظر است حاصل نمی آید زیرا که هدف از رده بندی، تلخیص و ساده نمودن اطلاعات آماری برای محاسبات است. یکی از روشها که برای طبقه بندی کردن داده ها به ما کمک می کند قاعده استورجس است.
– تعیین بعد طبقه
بعد از مشخص شدن تعداد طبقات، لازم است فاصله بین طبقات (h) تعیین شود. با توجه به دامنه تغییرات داده ها (R) و تعداد طبقه های به دست آمده که آن را با (K) نشان می دهیم این کار به سادگی امکان پذیر است.
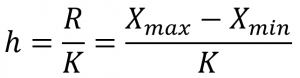
در محاسبه فاصله طبقات معمولاً نتیجه تقسیم را به عدد بعدی گرد می شود. این گرد کردن سبب می شود که تمام داده ها در جدول آورده شوند. چنانچه عمل تقسیم تعداد طبقات بر دامنه تغییر، بدون باقیمانده باشد یک طبقه دیگر به جدول اضافه می شود تا جدول در برگیرندۀ تمام داده ها باشد.
– انتخاب نقطۀ شروع
نقطه شروع می تواند کمترین نمره یا نمره ای کمی پایین تر از آن باشد چنین نقطه ای حد پایین اولین طبقه تعریف می شود.
– بعد طبقه به نقطه شروع اضافه شود
نقطه شروع را با بعد طبقه جمع کرده تا حدود پایین طبقه دوم حاصل شود. حدود پایین طبقه دوم را با بعد طبقه جمع کرده تا حدود پایین طبقه سوم به دست آید و به همین طریق ادامه داده می شود که حدود پایین تمام طبقات به دست آید.
 ناب لرنینگ |
بزرگترین بانک اطلاعاتی پروژه های دانشجویی
ناب لرنینگ |
بزرگترین بانک اطلاعاتی پروژه های دانشجویی