الگوریتم Apriori
الگوریتم اپریوری Apriori از اولین الگوریتم هایی است که جهت یافتن مجموعه اقلام تکرار شده از آن استفاده می شود. نام این الگوریتم برگرفته از شیو های است که از آن استفاده می کند، یعنی استفاده از دانش مرحله قبل که در ادامه آن را تشریح می کنیم. الگوریتم Apriori توسط اگراوال Agrawal و همکاران، در مرکز تحقیقات IBM Almaden کشف شد و می توان آن را برای تولید کلیه مجموعه اقلام تکرار شده بکار برد.
الگوریتم Apriori یک الگوریتم جستجوی سطحی است، که با پایان کاوش در مرحله k ام به مرحله بعدی یعنی k+1 می رود. این عمل تا محقق شدن شرط یا شروط پایانی تکرار می شود. در مرحله k ام مجموعه اقلام k تایی تولید خواهند شد. پس از محاسبه مقدار پشتیبان برای هرکدام و مقایسه آن با مقدار minsup الگوی های مکرر k تایی شناسایی می شود.
در مرحله بعدی الگوریتم با کمک الگوهای مکرر k تایی، مجموعه اقلام (k+1) تایی کاندید که بالقوه می توانند مکرر باشند را تولید می کند. به همین ترتیب با توجه به مقدار minsup برخی حذف شده و مجموعه اقلام مکرر (k+1) تایی تشکیل خواهند شد. این عمل تا یافتن آخرین مجموعه قلم مکرر ادامه پیدا می کند. این الگوریتم در حین اجرا از قاعدهای موسوم به قاعده Apriori استفاده می کند که بدین صورت بیان می شود: “اگر یک الگوی مکرر داشته باشیم، کلیه زیرمجموعه های آن نیز مکرر هستند.” به عبارت دیگر اگر مجموعه اقلام I مکرر نباشد، هر مجموعه ای که شامل I است نیز نمی تواند مکرر باشد.
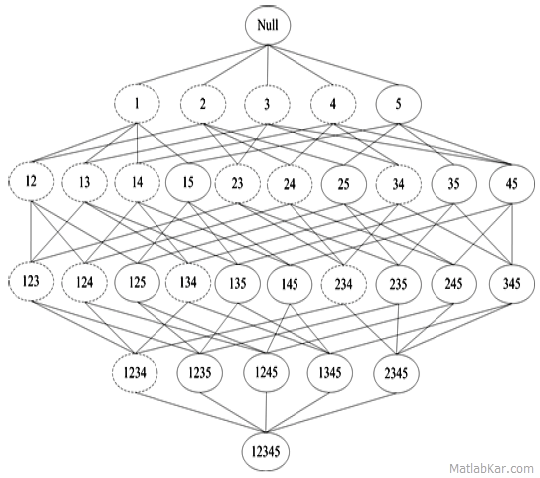
با کمک قاعده Apriori فضای جستجو کاهش مییابد. شکل زیر کل فضای جستجو را برای مجموعه اقلامی که از {۱,۲,۳,۴,۵} استفاده کرده است را نشان می دهد. برای سادگی الگوها به شکل یک عدد نمایش داده شده است. برای مثال الگوی {۱,۲,۳} را به صورت ۱۲۳ نشان داده ایم. دقت کنید که در شکل الگوهای مکرر با دایرههای خطچین مشخص شدهاند. با نگاه به الگوی مکرر {۱,۲,۳,۴} که در شکل به صورت ۱۲۳۴ نشان داده ایم، متوجه خواهید شد که همه زیرمجموعه های آن نیز مکرر هستند. یا اینکه کلیهی مجموعه اقلامی که شامل {۵} هستند، نمیتوانند مکرر باشند. چون {۵} مکرر نیست. بدین ترتیب استفاده از این استراتژی باعث کاهش فضای جستجو درتولید اقلام مکرر می شود.
قاعده Apriori به گروه خاصی از قواعد که دارای خاصیت پادیکنواختی هستند، تعلق دارد. این خاصیت به صورت خلاصه بدین صورت بیان می شود که اگر مجموعه نتواند در یک آزمون موفق باشد، کلیه اَبر مجموعه های آن نیز در همان آزمون با شکست مواجه می شوند.
فرض کنید J می تواند هر نمونه ای از مجموعه اقلامی باشد که از مجموعه I منتج می شود. یک مقیاس f دارای خاصیت یکنواختی است اگر:
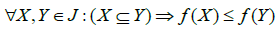
که نشان می دهد اگر X زیر مجموعه Y باشد، بنابراین f(X) نباید بزرگتر از f(Y) باشد. در مقابل f دارای خاصیت پاد یکنواختی است اگر:
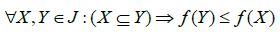
هر مقیاس و قاعد های همانند اپریوری (Apriori) که دارای خاصیت پاد یکنواختی است، می تواند برای الگوریتم های داده کاوی مثل تولید مجموعه اقلام مکرر موثر باشد. جدول زیر یک پایگاه داده تراکنشی با ۵ تراکنش و ۱۱ قلم داده را نشان میدهد. با تنظیم مقدار minsup برابر با 60 درصد و با کمک قاعده اپریوری می خواهیم الگوهای مکرر را در این پایگاه داده تولید کنیم.
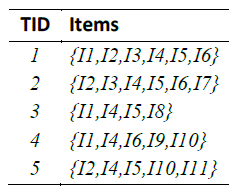
با پیمایش پایگاه داده ها و با توجه به مقدار minsup که برابر با 60 درصد (معادل ۳ تکرار از میان ۵ تراکنش) است، الگوهای مکرر ۱تایی یا یک عضوی بدست می آیند (شکل زیر). همانطور که در شکل زیر مشخص است از میان ۱۱ قلم داده فقط ۵ قلم مکرر هستند، که در ستون سوم جدول علامت خوردهاند. در مرحله دوم با کمک این مجموعه اقلام مکرر و الحاق آنها مجموعه اقلام کاندیدی تولید خواهند شد که می توانند بالقوه مکرر باشد.

چنانچه الگوریتم بدون توجه به اقلام مکرر ۱ تایی قصد تولید اقلام ۲ تایی را داشت، باید ۵۵ مجموعه قلم ۲ تایی را ایجاد می کرد.

این در حالی است که با کمک الگوهای مکرر ۱ تایی فقط تعداد ۱۶ مجموعه اقلام ۲ تایی ساخته شده است و این نکته کاهش فضای جستجو را نشان می دهد. در این مرحله نیز پایگاه داده برای محاسبه مقدار پشتیبان مجموعه اقلام ۲ تایی موجود در شکل بالا پیمایش می شود. پس از حذف مجموعه اقلام ۲ تایی که مقدار پشتیبان آنها از حد آستانه (مقدار ۳) کمتر است، مجموعه اقلام مکرر شناسایی می شوند. بعد از این با الحاق الگوهای مکرر ۲ تایی باید مجموعه اقلام ۳ تایی که مستعد مکرر بودن هستند، تولید شوند. دو نکته مهم در پیاده سازی این مرحله به بعد باید رعایت شود. در این مرحله شما مجاز به الحاق دو الگوی ۲ تایی هستید که نتیجه یک مجموعه اقلام ۳ تایی باشد.
 ناب لرنینگ |
بزرگترین بانک اطلاعاتی پروژه های دانشجویی
ناب لرنینگ |
بزرگترین بانک اطلاعاتی پروژه های دانشجویی